リターンとリスクに続いて、相関係数について考えてみたいと思います。
相関係数=2つの事象間の共分散をそれぞれの標準偏差で割ったもの(-1<
r <1)
つまり、異なる資産間のリスクの連動度を表す指標であると筆者は解釈しています。これを用いると、異なる資産を組み合わせた時の合成リスクを計算できます。
まず、合成リターンは資産配分ウェイトで重みづけした平均。
（式1）
一方合成リスクはまず以下の式を考える。
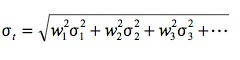（式2）
これは各事象が独立な場合の誤差伝搬式。いわゆる重みづけした自乗和のルート。これを相関係数を用いて一般化すると、
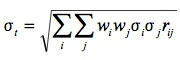（式3）
つまり相関係数をマトリックスとして総当たり的に和を取る。
結局、2式は3式の相関係数行列を単位行列にしたもの。また見方を変えると、相関係数の定義から、合成リスクは重みづけした共分散の和とも言える。
相関係数がすべて1ならば、合成リスクはリターンと同じく単純な重みつき平均ですが、相関係数が1より小さい場合は必ずそれより小さくなる点が肝です。
これから分散投資の有効性が導かれます。
（関連記事）
相関係数とσ（２）（追記）
