相関係数とσ(2)
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
コメント
ただいまコメントを受けつけておりません。
相関係数とσ(2)
相関係数とσのつづきです。
今回は、資産Aと資産Bという2資産の場合の合成リスクを計算したいと思います。 グラフは、資産Bの割合と、資産AB間の相関係数を変数として、合成リスクをプロットしたものです。
【ケース1】
リターンとリスクが異なる資産の場合(シャープレシオは等しいとした)
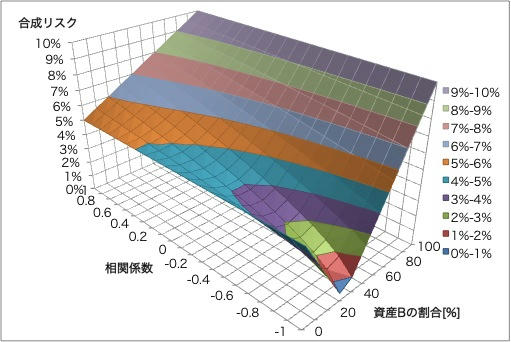
①相関係数=1の断面が、両者を単純に加重平均した合成リスクです。
②相関係数<1の場合、①よりも合成リスクが必ず小さくなっていることがわかります。
③特に、グラフのオレンジと水色の境界(5%)を下回る領域に注目です。これは資産Aを単独で持つ場合よりも、リスクの高い資産Bを組み入れた方がリスクが小さくなることを示しています。例えば、相関係数が0.3のとき、資産Bを20%組み入れても合成リスクは資産Aの5%と等しいままです。さらにそのときの合成リターンは2.4%となり、資産Aの2%より大きくなります。
次のグラフは、「資産Bの割合[%]」の軸をリターンに置き換えて、相関係数一定の断面を切り取ったものです。
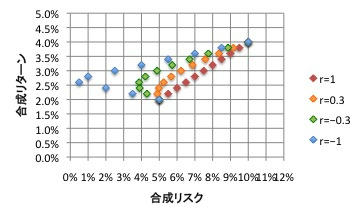
これがいわゆる効率的フロンティアと呼ばれる曲線です。
①相関係数=1では単純平均、つまり2資産を通る直線上にしか解がない。
②相関係数<1ならば、リスクが単純平均より小さくなる解(いわゆるパレート解)が存在することを示しています。
【ケース2】
リターンとリスクが等しい資産の場合

①ケース1と同様に相関係数<1の場合、合成リスクが必ず小さくなっていることがわかります。
②特に、相関係数が-1で50:50の割合で持った場合、合成リスクがゼロになっています。また相関係数が0.3ならば、合成リスクは8.1%まで下げることができます。
③この場合はリスクが下がってもリターンは変化しません。
以上が相関係数の意味です。ケース1からは相関係数によって効果的なリスク低減とリターン向上が望めること、ケース2からはリターンリスクが同じなら絶対に(デフォルト等を除いて)分散した方がよいことが示唆されます。
ただ、最近は世界の資産間の連動性が高まり、相関係数が1に近くなっています。米国が下がれば日本も下がる、などです。しかし完全に1にならない限りは効果があるので、分散投資は有効だと考えられます。
(関連記事)
相関係数とσ
今回は、資産Aと資産Bという2資産の場合の合成リスクを計算したいと思います。 グラフは、資産Bの割合と、資産AB間の相関係数を変数として、合成リスクをプロットしたものです。
【ケース1】
リターンとリスクが異なる資産の場合(シャープレシオは等しいとした)
| ケース1 | リターン | リスク |
|---|---|---|
| 資産A | 2% | 5% |
| 資産B | 4% | 10% |
①相関係数=1の断面が、両者を単純に加重平均した合成リスクです。
②相関係数<1の場合、①よりも合成リスクが必ず小さくなっていることがわかります。
③特に、グラフのオレンジと水色の境界(5%)を下回る領域に注目です。これは資産Aを単独で持つ場合よりも、リスクの高い資産Bを組み入れた方がリスクが小さくなることを示しています。例えば、相関係数が0.3のとき、資産Bを20%組み入れても合成リスクは資産Aの5%と等しいままです。さらにそのときの合成リターンは2.4%となり、資産Aの2%より大きくなります。
次のグラフは、「資産Bの割合[%]」の軸をリターンに置き換えて、相関係数一定の断面を切り取ったものです。
これがいわゆる効率的フロンティアと呼ばれる曲線です。
①相関係数=1では単純平均、つまり2資産を通る直線上にしか解がない。
②相関係数<1ならば、リスクが単純平均より小さくなる解(いわゆるパレート解)が存在することを示しています。
【ケース2】
リターンとリスクが等しい資産の場合
| ケース2 | リターン | リスク |
|---|---|---|
| 資産A | 4% | 10% |
| 資産B | 4% | 10% |
①ケース1と同様に相関係数<1の場合、合成リスクが必ず小さくなっていることがわかります。
②特に、相関係数が-1で50:50の割合で持った場合、合成リスクがゼロになっています。また相関係数が0.3ならば、合成リスクは8.1%まで下げることができます。
③この場合はリスクが下がってもリターンは変化しません。
以上が相関係数の意味です。ケース1からは相関係数によって効果的なリスク低減とリターン向上が望めること、ケース2からはリターンリスクが同じなら絶対に(デフォルト等を除いて)分散した方がよいことが示唆されます。
ただ、最近は世界の資産間の連動性が高まり、相関係数が1に近くなっています。米国が下がれば日本も下がる、などです。しかし完全に1にならない限りは効果があるので、分散投資は有効だと考えられます。
(関連記事)
相関係数とσ
コメント
カレンダー
最新記事
最新コメント
リンク
ブログ内検索
アーカイブ
ブログ内インデックス
プロフィール
HN:
Rocky
性別:
男性
職業:
技術系
PR
