時間とリスクの関係で触れたドルコスト平均法について考えます。

時間分散がどれくらい有効であるのかシミュレーションしてみました。

A．基準価額
年間10%上昇しつつ20%変動する相場をサインカーブと一次関数でモデル化。
B．平均取得価格
毎月一定金額買った場合。ドルコスト平均法を表す。
C．取得価格の平均
毎月一定口数買った場合。その時点までの基準価額の平均を表す。
D．最初にドカっと
最初に1年分買った場合。その時の基準価額を表す。

【ケース1】1年間相場が上昇し続けた場合。

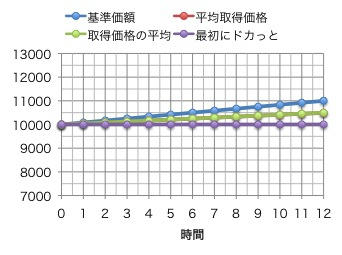
これはもうDはウハウハで笑いが止まりません。Bはいたずらに単価を引き上げてしまいます。

【ケース2】プラマイ半々の場合。

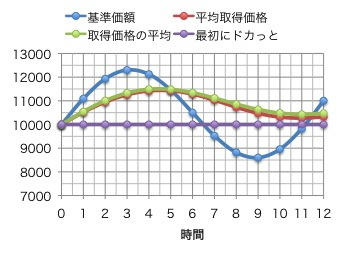
この場合もDが最も単価が低いですが、注目すべきはBとCの差が目立ってきた点です。

【ケース3】ケース2から1ヶ月タイミングがずれた場合。

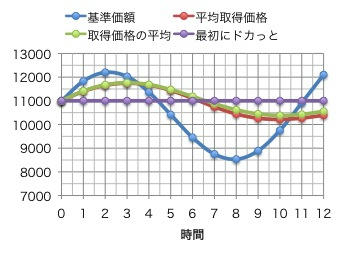
ちょうど今年のような相場をイメージしています。この場合、DよりもBの方が単価が低くなりました。特にDは5月あたりからモンモンとした気分を味わったに違いありません。一方Bはしめしめと安値で拾い上げたと思います。

ドルコスト平均法のまとめ
◆メリット
平均取得価格が取得価格の平均を必ず下回る
高値づかみを避けることができる
◆デメリット
平均リターンは毎年プラスなので、購入を遅らせた分リターンが減る可能性がある

以上のように一長一短があります。しかしながら、昨日の住宅統計で上げて今日の雇用統計で下げる。その統計や予想にどれだけ誤差が含まれているのか。市場の一喜一憂に我々が付き合う必要はありません。

またこの時間分散が自然に成立する方法が毎月の積立です。